Crittografia moderna

Crittografia a chiave pubblica o asimmetrica

Algoritmo Diffie-Hellmann

I cifrari tradizionali sono tutti caratterizzati da una chiave segreta; mittente e destinatario dei messaggi segreti devono preventivamente concordare una qualche chiave da mantenere segreta: una parola segreta (oggi la si direbbe una password) o una griglia o una qualche tabella di codifica. Per questo motivo essi sono altresì detti cifrari simmetrici.
Questa necessità di comunicarsi la chiave segreta è un grosso punto debole: o ci si vede di persona e in luogo riservato, o si deve usare un canale di comunicazione assolutamente sicuro, cosa molto difficile da ottenersi (e se si dispone di un tale canale … la crittografia diviene inutile); e la scoperta della chiave da parte del nemico sarebbe fatale alla segretezza del messaggio.

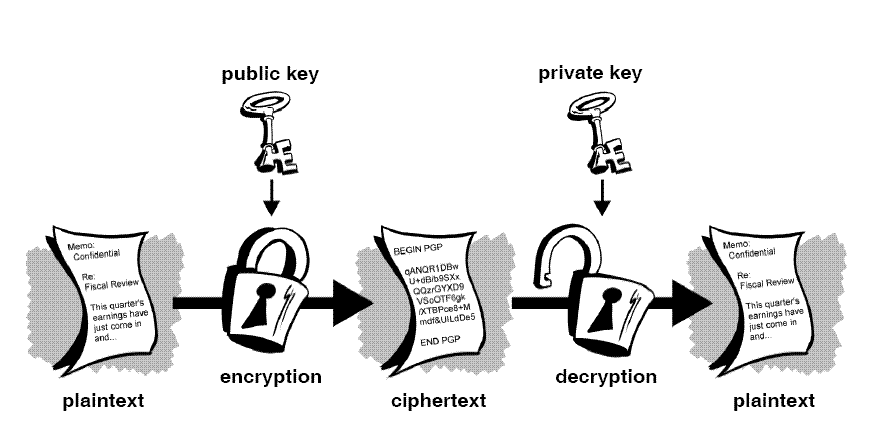
A partire dagli anni ’70 si sono affermati i cosiddetti cifrari a chiave pubblica, o cifrari asimmetrici, basati su una filosofia del tutto diversa: la chiave per cifrare non è la stessa di quella per decifrare; la prima può allora essere resa pubblica mentre solo la seconda resta segreta. L’algoritmo che ha permesso tutto questo è detto algoritmo Diffie-Hellman, dal nome dei due ideatori, Whitfield Diffie e Martin Hellman, che lo presentarono al mondo, in una pubblicazione dal titolo: New directions in Cryptography.

Supponiamo che chiunque voglia utilizzare tate algoritmo abbia un coppia di chiavi o keypair così composta:

• una chiave pubblica ( public key ) $E$ per cifrare;
• una chiave privata ( private key ), segreta, $D$ per decifrare;

con la seguente proprietà : non è possibile calcolare $D$ conoscendo $E$.

Esse sono tali che se $m$ è il messaggio in chiaro (plaintext), allora $c = E(m)$ è il messaggio cifrato (ciphertext), ottenuto dal messaggio $m$ usando la chiave $E$; e quindi $D(c) = D(E(m)) = m$ cioè applicando al messaggio cifrato $c$ la chiave $D$ ottengo il messaggio originario $m$.

Tutte le chiavi pubbliche sono utilizzabili pubblicamente, esse potrebbero essere immagazzinate in un archivio pubblico per esempio. Al contrario, le chiavi private sono tenute segrete e sono note solo ai proprietari.

I vantaggi della crittografia a chiave pubblica rispetto alla crittografia classica sono molteplici, ad esempio:

• non è necessario alcuno scambio di chiavi tra utenti;
• c’è bisogno di un numero relativamente piccolo di chiavi.

Infatti, usandi sistemi simmetrici, ogni coppia di utenti deve avere una chiave segreta personale; quindi se ci sono $n$ utenti, c’è bisogno di $n(n-1)/2$ chiavi diverse.

Invece usando un cifrario asimmetrico, ogni utente ha bisogno di due sole chiavi e solo una di queste deve essere tenuta segreta.

Allora il numero di chiavi necessario è $2n$, cioè doppio rispetto al numero di utenti. Per esempio, se ci sono 1000 utenti e questi volessero utilizzare un cifrario simmetrico sarebbero necessarie 499.500 chiavi, mentre con un cifrario asimmetrico basterebbero 2000 chiavi.

La crittografia a chiave pubblica è utile anche per generare le cosiddette firme digitali o elettroniche.
Un’applicazione reale del crittosistema a chiave pubblica Diffie-Hellman: l’algoritmo RSA.

Whitfield Diffie e Martin Hellman avevano, ormai, lanciato la sfida. Ora il problema era realizzare in pratica quanto D&H avevano teorizzato. La sfida venne raccolta e, nel 1977, tre persone diedero il più spettacolare contributo alla crittografia a chiave pubblica: Ronald Rivest, Adi Shamir e Leonard Adleman. Il loro lavoro durò per mesi durante i quali Rivest proponeva strade possibili, Adleman le attaccava e Shamir faceva o l’una o l’altra cosa. Nel maggio del 1977 essi furono ricompensati dal successo: avevano scoperto come una semplice parte della Teoria classica dei numeri poteva essere usata per risolvere il problema.
Ma prima di discutere dell’algoritmo RSA è necessario introdurre alcuni “semplici” concetti della teoria dei numeri.

Teorema di Eulero

L’algoritmo RSA è, infatti, una diretta applicazione di questo teorema.

Indichiamo con $f(n)$ la funzione phi di Eulero di un numero naturale $n$ il numero dei numeri naturali minori o uguali a $n$ che non hanno nessun fattore, tranne $1$, in comune con $n$. In altre parole, $f(n)$ è il numero dei numeri naturali minori di $n$ e primi con $n$.

$f(1)=1$; $f(2)=1$; $f(3)=2$; $f(4)=2$; ... $f(15)=8$ e cioè $1, 2, 4, 7, 8, 11, 13, 14$

La funzione di Eulero ha inoltre le seguenti proprietà:

• se $p$ è un numero primo, allora $f(p) = p – 1$;
• se $p$ e $q$ sono due numeri distinti, allora $f(pq) = (p – 1)(q – 1)$.

Ora possiamo enunciare il teorema di Eulero:
Siano $m$ e $n$ due naturali primi fra di loro e $k$ un intero non negativo ($k \geq 0$), allora:

$$m^{kf(n)+1}\mod n = m$$

a noi interessa però, in particolar modo, il caso in cui n è il prodotto di due numeri distinti; in questo caso il teorema si può enunciare come segue:

Sia $m$ un naturale, $p$ e $q$ due primi distinti e $k$ un intero non negativo, allora:

$$m^{k(p-1)(q-1)+1} \mod(p*q) = m$$

in altre parole se dividiamo $m^{k(p-1)(q-1)+1}$ per il numero $p*q$ otteniamo come resto $m$.

L’algoritmo di Euclide

Tale algoritmo viene usato per generare la chiave privata e la chiave pubblica di ogni utente; esso serve per calcolare il massimo comun divisore $MCD(a,b)$ di due numeri naturali $a$ e $b$ ( $ a \geq b$ ).

L’algoritmo di Euclide può essere descritto così, con un linguaggio simile a quello della programmazione:

EUCLIDE(a,b){
    if b = 0
        return a;
    else
        return EUCLIDE(a, a mod b);
}

Ad esempio:

$EUCLIDE(30, 21) = EUCLIDE(21, 9) = EUCLIDE(9, 3) = EUCLIDE(3, 0) = 3$.

Si nota come l’algoritmo richiama se stesso, cioè è ricorsivo, ma non all’infinito, infatti, il secondo decresce ad ogni ricorsione. Così l’algoritmo termina sempre con una risposta corretta.

A volte è necessario dover calcolare due coefficienti $x$ e $y$, non negativi, tali che:
$$
d = MCD(a, b) = ax + by
$$

allora bisogna considerare l’algoritmo di Euclide esteso, che prende in input, due numeri $a$ e $b$ e restituisce una tripla $(d, x, y)$ che soddisfa l’equazione precedente, cioè:

EUCLIDE-EX(a, b){
    if b = 0
        return (a, 1, 0);
    else{
        (d', x', y') = EUCLIDE-EX(b, a mod b);
        (d, x, y) = (d', x', y' - (a/b)y');
        return (d, x, y);
    }
}

Da ciò segue che se a e b sono due interi primi tra loro (cioè tali che $MCD(a, b) = 1$), allora esiste un intero $c$ tale che:

$$(b*c)\mod a = 1$$

Tale relazione dice che $c$ è l’inverso di $b$ modulo $a$, ciò segue da:
$$
d = MCD(a, b) = ax + by
$$

ponendo $d = 1$.

Quindi esistono due numeri interi $x$ e $y$ tali che: $1 = d = ax + by$.

Poiché $ax$ è multiplo di $a$, dividendo $by$ per $a$, otteniamo necessariamente come resto $1$, cioè:

$$b*y \mod a = 1$$

avendo posto $c = y$.

Come viene generata la coppia di chiavi (pubblica – privata) con l’algoritmo RSA ?

• vengono scelti due numeri primi $p$ e $q$ sufficientemente grandi;
• viene calcolato il prodotto: $n = p*q$;
• viene calcolato: $f(n) = f(pq) = (p – 1)(q – 1)$;
• viene scelto un ulteriore numero e primo con $f(n)$;
• viene calcolato $d$ tale che: $e*d \mod f(n) = 1$.

A questo punto la coppia di chiavi è pronta: infatti $e$ ed $n$ costituiscono la chiave pubblica e $d$ la chiave privata.

Come funziona in pratica l’algoritmo RSA ?

Supponiamo che l’utente A voglia mandare un messaggio cifrato con RSA all’utente B. Prima di tutto A deve conoscere la chiave pubblica di B, e cioè la coppia di numeri $n$ ed $e$.

Poi il messaggio deve essere trasformato in una sequenza di uno o più interi positivi $m$ non maggiori di $n$ ($m \leq n$).

Ciò, all’apparenza, può sembrare arduo, ma basti pensare che i computers rappresentano i caratteri (lettere, numeri e caratteri speciali) ciascuno come uan sequenza di 8 bits; ad esempio:

• A = 01000001 ($base_{10}=65$, $base_{16}=41$),
• B = 01000010 ($base_{10}=66$, $base_{16}=42$),
• ...
• 0 = 00110000 ($base_{10}=48$, $base_{16}=30$),
• 1 = 00110001 ($base_{10}=49$, $base_{16}=31$),
• ...

in base allo standard ASCII ( American Standard Code for Information Interchange ) .

Ecco la Tabella Ascii in Esadecimale e Decimale

   2 3 4 5 6 7        30 40 50 60 70 80 90 100 110 120
  -------------      ---------------------------------
0:   0 @ P ` p     0:    (  2  <  F  P  Z  d   n   x
1: ! 1 A Q a q     1:    )  3  =  G  Q  [  e   o   y
2: " 2 B R b r     2:    *  4  >  H  R  \  f   p   z
3: # 3 C S c s     3: !  +  5  ?  I  S  ]  g   q   {
4: $ 4 D T d t     4: "  ,  6  @  J  T  ^  h   r   |
5: % 5 E U e u     5: #  -  7  A  K  U  _  i   s   }
6: & 6 F V f v     6: $  .  8  B  L  V  `  j   t   ~
7: ' 7 G W g w     7: %  /  9  C  M  W  a  k   u  DEL
8: ( 8 H X h x     8: &  0  :  D  N  X  b  l   v
9: ) 9 I Y i y     9: '  1  ;  E  O  Y  c  m   w
A: * : J Z j z
B: + ; K [ k {
C: , < L \ l |
D: - = M ] m }
E: . > N ^ n ~
F: / ? O _ o DEL

Una volta ottenuto il “valore numerico” del nostro messaggio, l’operazione che si esegue per cifrare $m$ è:
$$
c = m^{e} \mod n
$$
e quindi $c$ è il testo cifrato corrispondente al testo in chiaro $m$.
$$
m’ = c^{d} \mod n
$$
Si dimostra che $m’$ è proprio $m$, cioè il messaggio originario.

La robustezza dell’algoritmo RSA

Ci si domanda:

• E’ possibile dedurre la chiave privata da quella pubblica?
• E’ possibile decifrare un messaggio senza conoscere la chiave privata?

Supponiamo di conoscere la chiave pubblica, cioè i due numeri $n$ ed $e$ . Come si può risalire a $d$ cioè alla chiave privata? Ovviamente se si conoscesse $f(n)$, si potrebbe ottenere $d$ (è quello che succede quando si genera la coppia di chiavi). Quindi “basterebbe” calcolare $f(n)$. Ma come si può ricavare $f(n)$ ? Se si conoscesse la scomposizione di $n$ nei suoi fattori primi $p$ e $q$ , allora facilmente si potrebbe calcolare $f(n) = f(pq) = (p – 1)(q – 1)$. Si noti che anche il viceversa è vero: se, infatti, si conoscessero $n$ e $f(n)$ allora si potrebbe fattorizzare $n$, basterebbe risolvere il sistema formato dalle equazioni:
$$
\begin{cases}p*q = n \ (p – 1)(q – 1) = f(n) \end{cases}
$$
nelle due incognite $p$ e $q$ . Da quanto detto si deduce che calcolare $f(n)$ è equivalente a fattorizzare $n$ .

Problema della fattorizzazione

Il problema della fattorizzazione, cioè trovare i fattori primi di un numero, è uno dei più vecchi della teoria dei numeri. Attualmente esistono diversi algoritmi usati per fattorizzare, come ad esempio:

• Quadratic sieve. Questo è l’algoritmo più veloce conosciuto per numeri con meno di 150 cifre decimali. Una versione più veloce di questo algoritmo è chiamata Multiple polynomial quadratic sieve. La versione più veloce di questo algoritmo è chiamata Double
• Large prime variation of the multiple polynomial quadratic sieve.
• Number field sieve. Questo è l’algoritmo di fattorizzazione conosciuto più veloce. Quando fu proposto non era molto pratico, ma c’è stato un cambiamento dovuto alle implementazioni degli ultimi anni.
• Elliptic curve method. Questo metodo è stato molto usato per trovare fattori di numeri di 38 cifre, ma non più grandi. Per numeri più grandi gli altri algoritmi sono più veloci.
• Trial division. Questo è il più vecchio algoritmo di fattorizzazione, ed implica il controllo di ogni numero minore o uguale della radice quadrata del numero candidato.
• p-1 Method. Questo algoritmo è utile quando il numero da fattorizzare ha un fattore $p$ tale che $p-1$ ha solo fattori piccoli.

Ma si potrebbe pensare che visto che esistono tutti questi algoritmi che si occupano di fattorizzare un numero, allora in cosa consiste la sicurezza di RSA. E’ molto semplice. l’operazione di fattorizzazione è un’operazione che richiede moltissimo tempo anche avendo una grande potenza di calcolo. Inoltre i precedenti algoritmi perdono di efficacia se devono fattorizzare un numero prodotto di due primi dello stesso ordine di grandezza.

I migliori algoritmi di fattorizzazione noti non sono polinomiali ma subesponenziali. Il tempo $T(n)$ che impiegano (nel caso peggiore in cui $n$ sia il prodotto di due primi di uguale lunghezza) è proporzionale a:
$$
e^{\sqrt{\log{n}*(\log{\log{n}})}}
$$.

Utilizzando questa formula si vede che se per fattorizzare un numero di 100 cifre occorre un tempo $Q$, per fattorizzarne uno di 200 il tempo sale a circa 50.000.000 $Q$, e per 300 arriviamo a 60.000.000.000.000 $Q$. Se $Q$ è un secondo, per un intero di 100 cifre occorre 1 secondo, per 200 cifre più di un anno e mezzo, per 300 cifre 2 milioni di anni. Facciamo qualche esempio:
$$
F_9 = 2^{2^{9}} + 1 = 2^{512}+1
$$

Nel 1990 fu fattorizzato il nono numero di Fermat. Fu scoperto che questo numero, che ha 513 bits ( 155 cifre decimali ) è il prodotto di tre numeri primi aventi 7, 49, 99 cifre decimali.

Il 22 agosto 1999 si è fattorizzato RSA-155 un numero di 512 bits, e cioè:

1094173864157052742180970732204357612003732945449205990913842131476349984288934784717997257891267332497625752899781833797076537244027146743531593354333897

e si è scoperto che è il risultato del prodotto di due numeri primi:

#1 102639592829741105772054196573991675900716567808038066803341933521790711307779
#2 106603488380168454820927220360012878679207958575989291522270608237193062808643

Recentemente, il 3 dicembre del 2003, è stato fattorizzato RSA-576

188198812920607963838697239461650439807163563379417382700763356422988859715234665485319060606504743045317388011303396716199692321205734031879550656996221305168759307650257059

un numero di 576 bit, 174 cifre decimali, prodotto di due primi di 87 cifre:

#1 398075086424064937397125500550386491199064362342526708406385189575946388957261768583317
#2 472772146107435302536223071973048224632914695302097116459852171130520711256363590397527

Sebbene questi numeri siano stati fattorizzati, ciò è stato possibile solo grazie a una grande potenza di calcolo. Ad oggi, non si conosce un algoritmo “veloce” per fattorizzare; d’altra parte non è stato possibile dimostrare che un tale algoritmo non esiste. Sembra che il problema della fattorizzazione sia tanto difficile da non permettere neanche di provare che è difficile.

Concludendo per forzare RSA è necessario fattorizzare $n$; ad oggi, infatti, non è noto alcun altro attacco all’algoritmo RSA. Quindi la sicurezza di RSA è basata sulla difficolatà di fattorizzare un numero con centinaia di cifre. Oggi le chiavi RSA generate dai software di crittografia hanno una dimensione minima consigliata di 2048 bits, ma se ne possono generare anche con una dimensione di 3072 o 4096 bits. Chiavi RSA con dimensioni superiori a 4096 bits sono possibili ma poco pratiche.

I pro e i contro e le soluzioni usate nella pratica

Il vantaggio dei cifrari a chiave pubblica è evidente; non è più necessario concordare una chiave segreta, è sufficiente avere un elenco di chiavi pubbliche. Lo svantaggio di questi metodi è che, richiedendo un gran numero di pesanti calcoli matematici, la trasmissione è molto più lenta di quella tradizionale. Per questo la soluzione oggi più usata è quella di utilizzare una combinazione dei due metodi: il messaggio in chiaro viene cifrato con un algoritmo simmetrico, ( AES, 3DES, TWOFISH, BLOWFISH, CAST-256 ecc..) e una password generata a caso; quindi usando un cifrario a chiave pubblica (RSA, DH-ELGAMAL), si invia la password cifrata, ad esempio, con RSA, seguita dal messaggio cifrato.

Fonti

• www.crittologia.eu (a cura di Paolo Bonavoglia)
• David Kahn, The Codebreakers. The story of secret writing, Scribner, New York (1996)
• Simon Singh, Codici & Segreti, Rizzoli, Milano (1999)
• Albrecht Beutelspacher - Luigia Berardi, Crittologia. Come proteggere le informazioni riservate, Franco Angeli, Milano (1996)